A Python 3 package to efficiently compute non-Markovian open quantum systems.

About Us

We are both PhD students (one recently finished) in the Keeling/Lovett groups at the University of St Andrews where our work has focused on building tensor network algorithms to simulate non-Markovian open quantum systems. We began developing the OQuPy package to open up these methods to a much wider audience by placing the complex algorithms behind a simple and intuitive interface. We applied to the Unitary Fund to help support the extension of OQuPy to include a few new tools for open quantum systems analysis recently developed in our groups. We’ll get on to those but first a brief background on the key ideas.

About OQuPy

When an open quantum system is strongly coupled to a structured environment, describing the dynamics of that system becomes a challenging problem. Moreover, traditional approaches, based on time evolution of the reduced density matrix are generally not able to correctly calculate higher-order or multi-time correlations. In the past few years tensor network techniques based on an influence functional approach have been developed to address both these issues [1-5]. Here the tensor network representation is used to efficiently capture the non-Markovianity or “memory effects” that arise from the non-trivial coupling. This efficient representation lies at the heart of the OQuPy package and is what every module builds upon.

Extending OQuPy

Beyond the core functionality there have been a number of extensions developed in recent years that, while proven effective in published work, were relatively detached from the existing package and lacked a well maintained code base. Here we will focus on two of these:

1. Calculation of bath correlations from system correlations
2. Non-perturbative simulation of a system coupled to multiple environments

We decided to add these to the OQuPy package with hope that they would further attract new users who might find some use of these in their own research. The first of these allows further characterisation of the behaviour of an open quantum system by giving insight into the specific role of the environment which can become increasingly significant in cases of strong coupling. The second gives the user the possibility to account for strong coupling to multiple environments and examine the effect of their interplay on the system’s evolution. Thanks to the Unitary Fund we were able to support the implementation of these to OQuPy. We will now briefly cover the background to both these features and how they currently fit into the package.

Bath Dynamics

It has long been accepted that in simulating open quantum systems one must typically trace over the environmental degrees of freedom and thus lose access to the wealth of information contained in them. In the weak coupling limit this is of little consequence as we would generally expect the environment to be effectively stationary and not be doing much interesting. However, as the coupling is increased the role of the environment becomes increasingly significant. In this regime correlations can build between the system and environment which lead to complex behaviour in the system observable dynamics. When we trace over the environment in this case we are obscuring half of an intricate back-and-forth between system and surrounding. Fortunately, all is not lost. In fact it was shown in Ref [6] that, for a linearly coupled Gaussian environment, any correlation functions of the bath can be expressed purely in terms of the system correlation functions.

We have added a module bath_dynamics.py to the OQuPy package which currently contains a TwoTimeBathCorrelations class. This allows calculation of any second-order bath correlation function of a given model. Any necessary system correlation functions are computed and then stored for re-use on future bath correlation calculations. Check out this tutorial for a demonstration.

Multiple Environments

There are many processes in reality that can be modelled as a finite system coupled to independent baths. Quantum dots driven by an optical field often couple strongly to the vibrational degrees of freedom of their host material too. Looking to nature: photosynthetic complexes often display strong coupling between their electronic and vibrational degrees of freedom and of course are coupled as well to photons from the Sun. Were both baths coupled weakly then typically their effects on the system are treated additively, as if the the other bath didn’t exist. However, when either bath is strongly coupled this additive treatment can break down. When a quantum system is strongly coupled to a single bath it begins to make less sense to talk about them as distinct entities and rather consider hybrid excitations of correlated states between them. For example in light-matter coupling we may consider working in a polariton basis or similarly a polaron basis for strong electron-phonon coupling. When we introduce a second bath, even though independent from the first and potentially weakly coupled, it unavoidably interacts with the strongly coupled first bath via these correlated states. In Ref. [7] it was shown how we can extend the base algorithm to capture the non-additive effects of multiple environments.

This multi-environment feature was implemented in OQuPy with minimal adjustment of the existing code. One can simply follow the procedure for building a process tensor (as outlined here) of each environment and then submit them in a list to the compute_dynamics function.

Further and Future Extensions

Beyond the features covered above we recently added modules that allow the user to simulate chains of open quantum systems (each coupled to their own environment) by using tensor network representations to efficiently capture temporal and spatial correlations [8]. Further to this we hope to soon have a mean-field extension of TEMPO added where the number of degrees of freedom is reduced analytically through a supression of correlations between identical systems [9].

We sum up the current functionality of OQuPy in the following graphic:

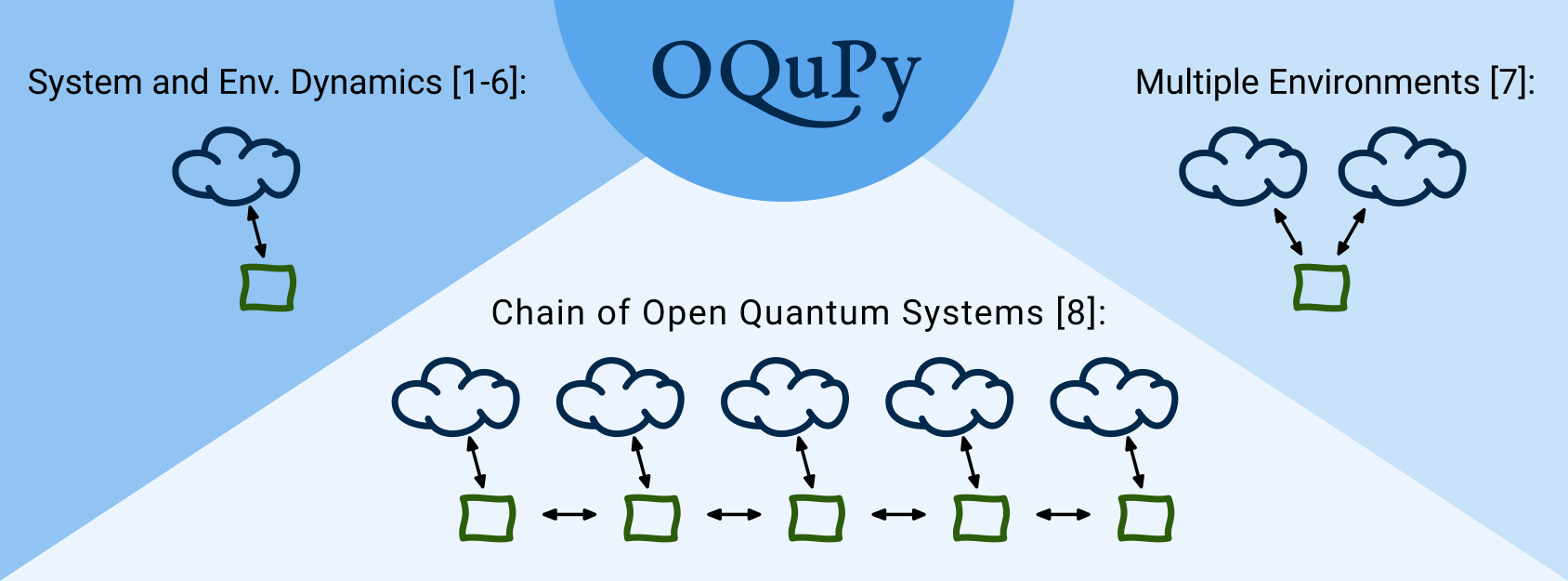
If you have any questions or suggestion please don’t hesitate to get in touch and post an issue on GitHub!

References

• [1] Strathearn et al., New J. Phys. 19(9), 093009 (2017).
• [2] Strathearn et al., Nat. Commun. 9, 3322 (2018).
• [3] Pollock et al., Phys. Rev. A 97, 012127 (2018).
• [4] Jørgensen and Pollock, Phys. Rev. Lett. 123, 240602 (2019).
• [5] Fux et al., Phys. Rev. Lett. 126, 200401 (2021).
• [6] Gribben et al., arXiv:2106.04212 (2021).
• [7] Gribben et al., PRX Quantum 3, 010321 (2022).
• [8] Fux et al., arXiv:2201.05529 (2022).
• [9] Fowler-Wright et al., arXiv:2112.09003 (2021).